Cosmology with space-based observatories

At 2pm, room E349, Eemeli Tomberg (Lancaster University), will be talking about
Quantum fluctuations from cosmic inflation give rise to the macroscopic structures of the universe. The strongest fluctuations collapse into primordial black holes, a dark matter candidate and a possible source of gravitational waves. Stochastic inflation is a tool to compute the fluctuation statistics non-perturbatively, needed for accurate black hole predictions. I discuss recent progress in these computations, their numerical implementation and analytical approximations, and the implications for black hole abundance in single-field models of inflation.
]]>
Hopes of Big Bang Discoveries Ride on a Future Spacecraft
More details can be found in the scientific paper Ref. [1] and this post.
]]>Primordial black holes (PBH) are cosmological objects that could have been formed in the earliest instants of the universe’s history, for instance, when large overdensities collapse under their own gravity. Understanding how these PBHs cluster is essential as it can provide insights into the evolution of structure formation in the universe and could potentially help in assessing how much, and when, binaries of these objects appear.
In Ref. [1], Pierre and Baptiste have used the excursion-set formalism to quantify the initial spatial clustering of PBHs generated from large Gaussian density fluctuations. Their method takes into account the “cloud-in-cloud” mechanism, which is a critical aspect that is overlooked in studies using the Poisson model of clustering.
In the excursion-set formalism, the collapse of an overdensity to form a PBH of mass \(M\) is recast into the probability of finding the first crossing of a random walk at some scale \(S(M)\). This approach has been already applied to study the formation of large-scale structure, in which multiple crossings of a random walk describe a hierarchy of structures. This formalism was first developed to solve the “cloud-in-cloud” problem, that is resolving this hierarchy of structures.
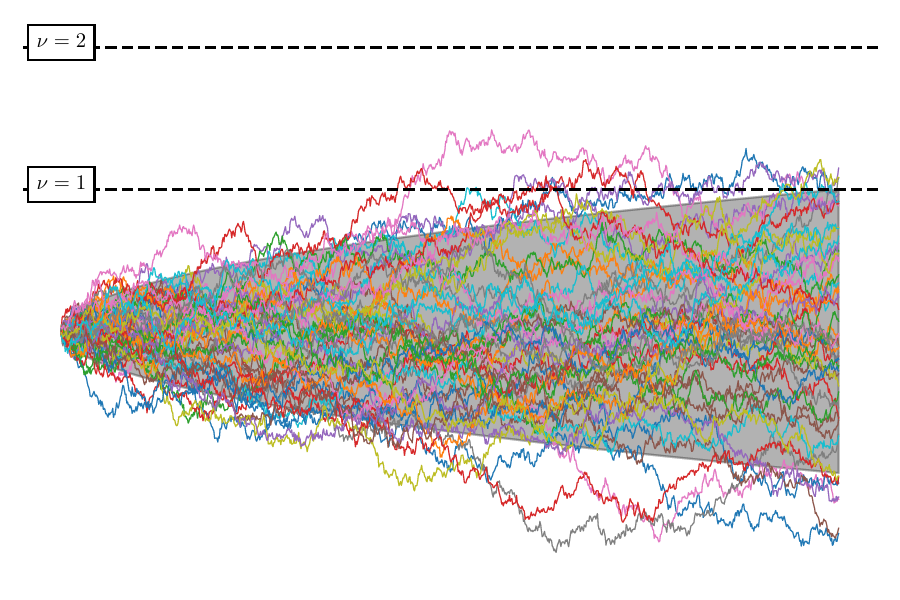
The cloud-in-cloud mechanism implies that PBHs should be part of larger structures: they don’t just appear randomly as per the Poisson assumption. This results in a natural and intrinsic correlation between the formation of pairs of PBHs, which is important for accurately modelling the clustering behaviour at small scales. The following picture shows two random walks that share a common past until the “time” \(S_{r}\): they come from the same realisation of a large scale density perturbation. Subsequently, they evolve in distinct ways and this results in two different collapses that occur respectively at the first-crossing times \(S_{1}\) and \(S_{2}\)

Such an approach automatically includes short-range exclusion effects: PBHs are anti-correlated at short distances!
The authors also present explicit expressions for the excess probability to find pairs of PBHs separated by a given distance and for the excess probability to find pairs with an asymmetric mass ratio.
]]>
LISA will be the next-generation observatory in the field of gravitational waves, surpassing current terrestrial capabilities by exploring lower frequencies and longer timescales, opening up a new observation window into the universe. and technological innovation. The LISA definition study report, in which Pierre was a contributor, presents an in-depth analysis of the mission’s scientific rationale, design, and implementation plans, see Ref. [1]. It highlights the groundbreaking discoveries that LISA is expected to make
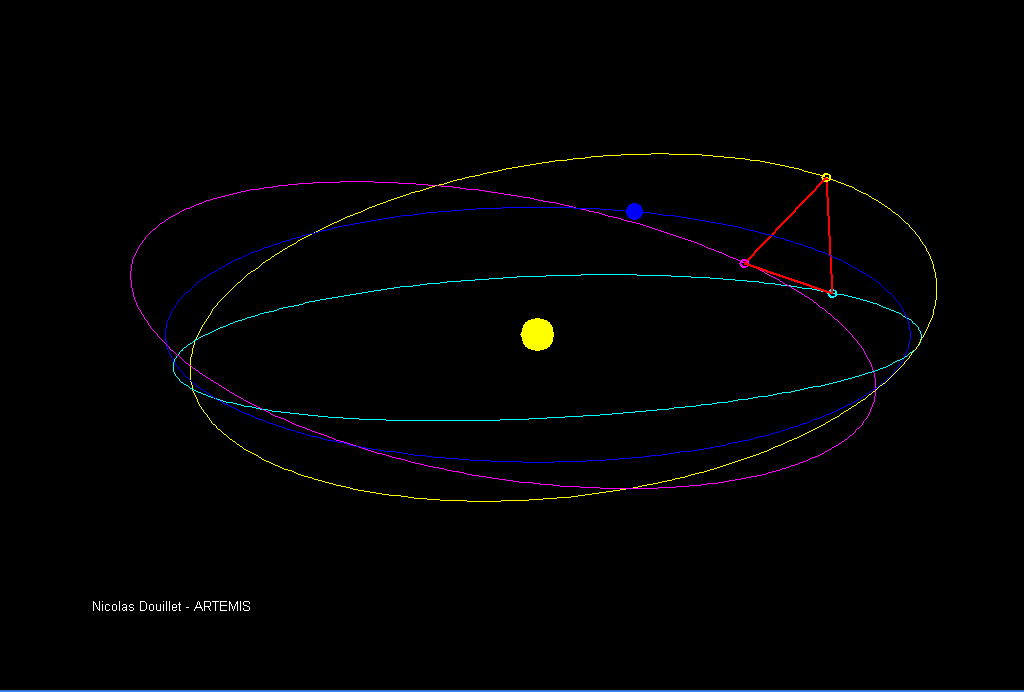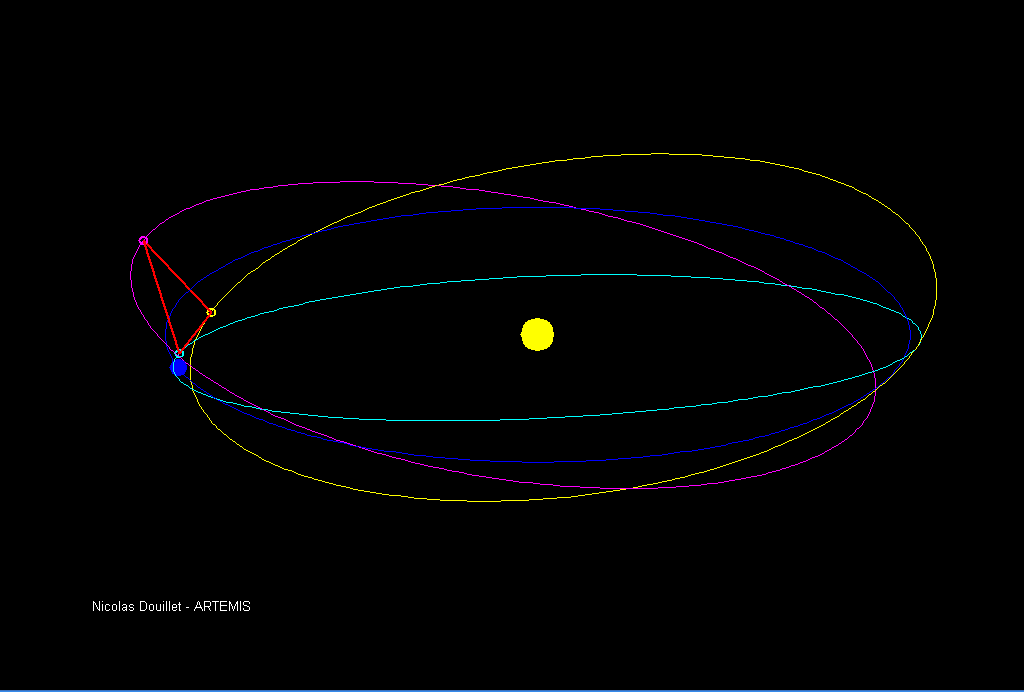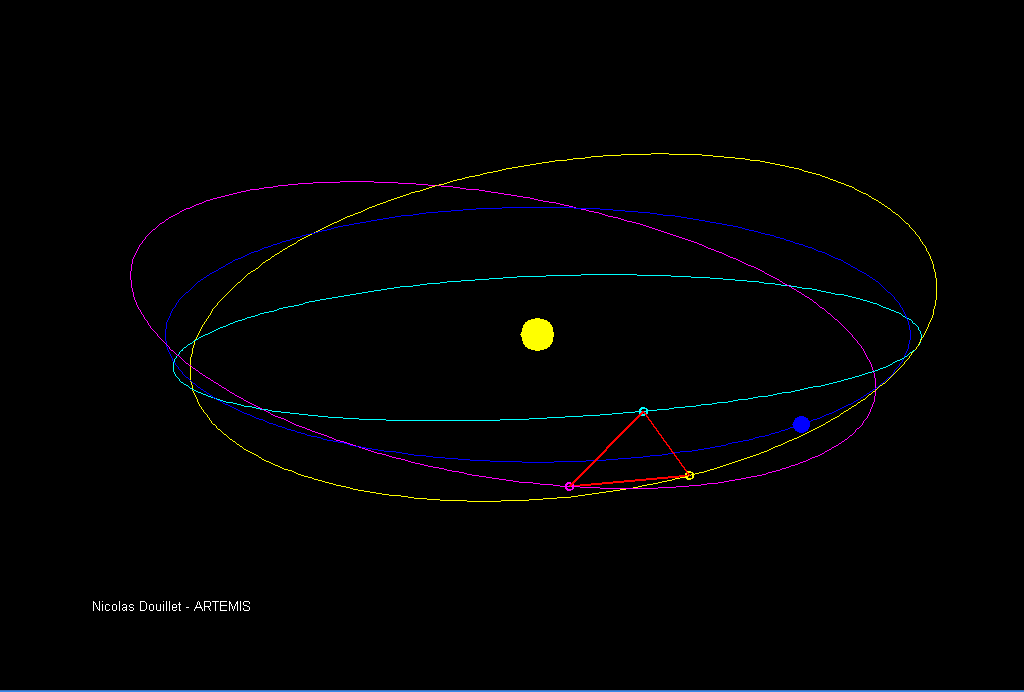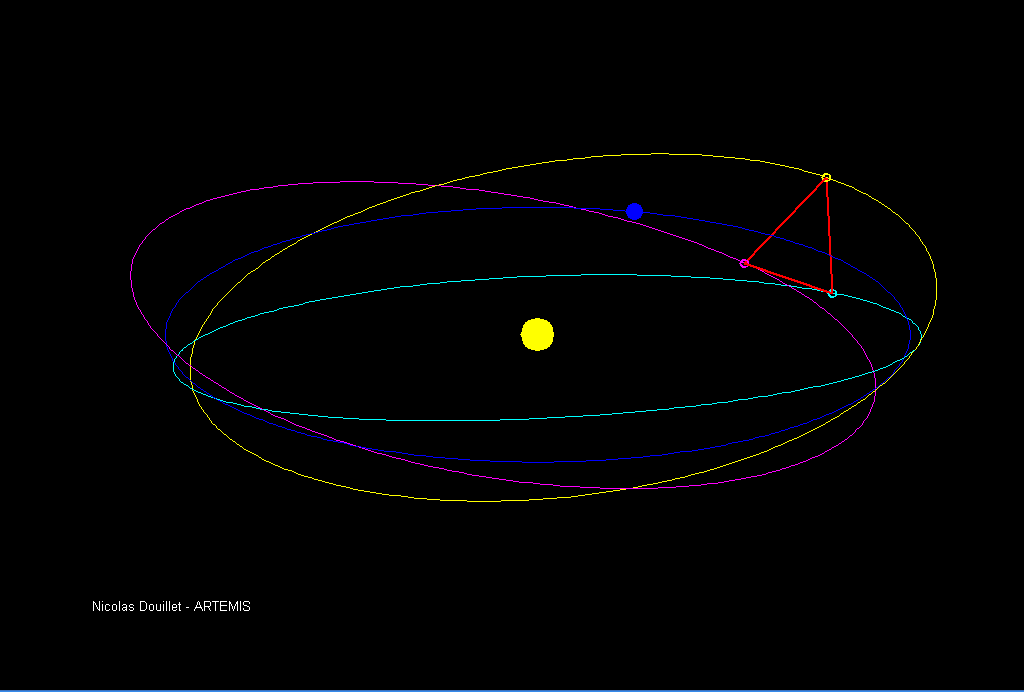
With ESA’s approval, the LISA mission moves one step closer to reality!
]]>Applicants interested in early universe cosmology (cosmic inflation, reheating, cosmic defects…), CMB, large scale structures, gravitational waves cosmology, as well as data analysis for current and future cosmological observations (CMB-S4, Euclid, LiteBird, LISA…), are particularly encouraged to apply. A summary of our research interests can be consulted online.
Appointment is available for two years. Please notice that applicants should have obtained their PhD no longer than 5 years before the starting date of the fellowship, plus one year of allowance for parenthood.
Letters of application (including a curriculum vitae, a list of publications, a brief statement of research interests) and at least two recommendation letters from senior scientists should be submitted on-line, by the 28th of January 2024, at:
https://cp3.irmp.ucl.ac.be/job/94
For more information, or postal applications, please contact:
christophe.ringeval@uclouvain.be
Cosmology, Universe and Relativity at Louvain
Institute of Mathematics and Physics
Louvain University
2, Chemin du Cyclotron
1348 Louvain-la-Neuve
Belgium
Applicants with expertises in cosmic inflation, large scale structures, data analysis and Bayesian inference, skilled in computing and analytics, are particularly encouraged to apply.
The position is supported by the Belgium Euclid Science Exploitation ESA-Prodex research program which unifies expertises between Ugent (Gent), ULiege (Liège), ULB (Brussels) and UCLouvain (Louvain-la-Neuve) universities. There will be close collaborations between these groups, computing and travelling support are excellent.
Appointment is available for three years.
Letters of application (including a curriculum vitae, a list of publications, a brief statement of research interests) and at least two recommendation letters from senior scientists should be submitted on-line, by the 28th of January 2024, at:
https://cp3.irmp.ucl.ac.be/job/95
For more information, or postal applications, please contact:
christophe.ringeval@uclouvain.be
Cosmology, Universe and Relativity at Louvain
Institute of Mathematics and Physics
Louvain University
2, Chemin du Cyclotron
1348 Louvain-la-Neuve
Belgium
It is a common Cosmologist’s intuition that cosmological fluctuations, the tiny perturbations of amplitude \(10^{-5}\) at the origin of galaxies, should induce some kind of noise on the cosmological parameters. Is this quantifiable? Are super-Hubble cosmological perturbations having an effect at all?
In Ref. [1], we show that arbitrarily long perturbations have an observable effect. More precisely, the gradient and Laplacian of these fluctuations are dynamically creating a spatial curvature in the homogeneous and isotropic metric of local observers. In the following picture, we sketch how one of these modes, having a wavelength much larger than the observer’s Hubble radius, can be “felt” through its gradient.

It is not a few Hubble-sized fluctuations that contribute, but an infinite number of super-Hubble modes, all those having wavelength larger than our observable universe. Denoting by \(K\) the curvature of the FLRW spatial sections, and \(\xi\) the sum of these constant modes, we find
\[K = -\frac{2}{3} \Delta \xi - \frac{1}{3} \left(\nabla \xi \right)^2.\]However, because fluctuations are, by definition, of random nature, we cannot predict a definite value for the curvature density parameter \(\Omega_\mathrm{K_0}\). This one is now promoted to a stochastic variable. Even though the sum of all super-Hubble modes averages to zero, i.e. \(\langle \xi \rangle = 0\), we predict, for the standard Gaussian and scale-invariant cosmological perturbations, a very small non-vanishing value
\[\langle \Omega_\mathrm{K_0} \rangle = -\frac{\langle K e^{-2\xi} \rangle}{a_0^2 H_0^2} = \frac{5}{6} \mathcal{P}_* \simeq 1.7 \times 10^{-9}.\]More importantly, because \(\Omega_\mathrm{K_0}\) is a stochastic variable, it also fluctuates and its realizations are, in fact, dictated by its standard deviation
\[\sqrt{\langle{\Omega_\mathrm{K_0}^2}\rangle-\langle{\Omega_\mathrm{K_0}}\rangle^2} \simeq \dfrac{1}{3} \sqrt{\mathcal{P}_*} \simeq 1.5 \times 10^{-5}.\]This is the typical value that any observer will measure at any epoch during the cosmic history.
But there is more. The spatial curvature of our local Hubble patch is thus a measurable number that can tell us what is going on on the largest possible length scales of the Universe, length scales that are much larger than our Hubble volume. What if the infinite sum of very large wavelength modes, \(\xi\) here, is no longer a small quantity? Such a situation could very well be happening if the Universe has experienced a period of stochastic inflation in its infancy!
In Ref. [1], we have been able to estimate the full probability distribution function for \(\Omega_\mathrm{K_0}\) when cosmological fluctuations are generated by Cosmic Inflation. If \(\xi\) remains small, it is a slightly distorted Gaussian distribution with a typical width of \(10^{-5}\), as expected. But if inflation last for a long period, enough for \(\xi\) to be of order unity, the distribution becomes highly non-Gaussian, as represented in the following figure (red curve)
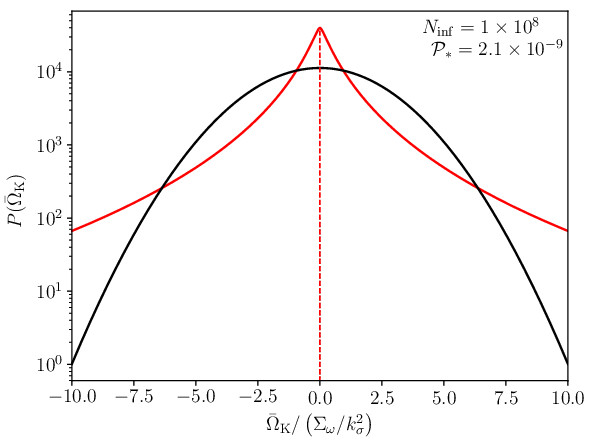
In this plot, the black curve is what would be a Gaussian probability distribution with same width. Clearly, large values of \(\Omega_\mathrm{K_0}\) are now much more probable than what one could have naively expected. Are we going to measure a non-vanishing \(\Omega_\mathrm{K_0}\) in the future?
]]>At 2pm, room E349, Bryce Cyr (University of Manchester), will be talking about
In this talk, I will discuss various ways in which distortions to the frequency spectrum of the cosmic microwave background can be used to place constraints on stochastic backgrounds of gravitational waves. After a brief overview of spectral distortion theory, I will show how enhancements to the small-scale primordial power spectrum of curvature perturbations can induce sizeable distortions. Even in the absence of enhancements, a nearly-scale invariant spectrum presents a target well within reach of next generation experiments. Additionally, I will highlight how the presence of primordial tensor modes will also lead to an inevitable (although small) distortion signature. I will then apply this formalism to a model of scalar induced gravitational waves (SIGWs), showcasing how constraints on the primordial scalar power spectrum can be mapped to the gravitational wave parameter space for these models. Time permitting, I will also show our updated formalism can be used to improve constraints on the parameter space of primordial black holes.
]]>