In collaboration with Konstantinos Dimopoulos from the University of Lancaster, Eemeli has studied the possibility of eternal inflation in models that produce primordial black holes.
Cosmic inflation is a period of accelerated expansion of space which likely took place in the very early universe. The expansion is driven by the inflaton, a scalar field that undergoes random motion due to quantum effects. This random motion shows up as inhomogeneities in the late universe, seeding cosmic structure such as galaxies and galaxy groups. If the inhomogeneities are particularly strong at short scales, they may form structures even before galaxy formation, collapsing straight into primordial black holes. Such black holes would be dark matter and would radiate gravitational waves that could be observable by gravitational wave detectors.
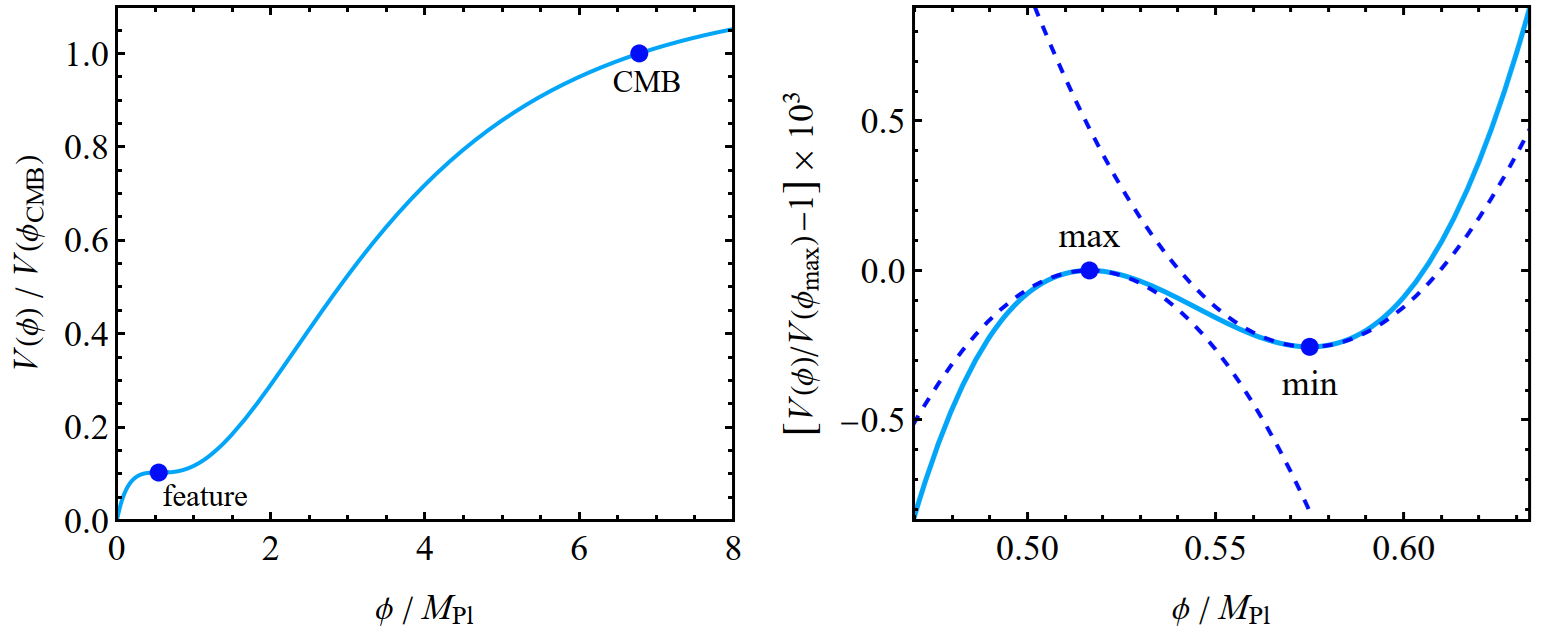
A popular way to produce the strong inhomogeneities needed for black hole formation is to give the inflaton an inflection point potential with a local bump (see figure). As the inflaton climbs over the bump, it slows down, so the quantum fluctuations can have a stronger relative effect. Besides black holes, such strong quantum effects may lead to another phenomenon: eternal inflation. In eternal inflation, quantum kicks oppose classical forces enough to keep the inflaton near the bump eternally in some regions of space.
To test if inflation is eternal in primordial black hole models, in Ref. [1], we solved the Fokker-Planck equation, which describes the time evolution of the inflaton’s probability distribution (\(N\) is the time variable):
\[\partial_N P(\phi,N) = \partial_\phi\left\{\partial_\phi\left[\frac{1}{2} \sigma^2(\phi) P(\phi,N)\right] - \mu(\phi) P(\phi,N)\right\} .\]The classical drift \(\mu\) and the quantum diffusion coefficient \(\sigma\) depend on the model, but take universal forms near the potential’s local minimum and maximum, which are most important for eternal inflation. We were able to show that eternal inflation happens generically near the minimum if field variations are Planckian, \(\phi \sim M_\text{Pl}\), and also near the maximum if the potential’s second derivative there is not too large in magnitude, \(|V''(\phi)| \leq 6V(\phi)/M_\text{Pl}^2\). We checked these conditions against three typical models from the literature, and they were satisfied in all three cases. Eternal inflation is a generic consequence of such inflection point models.
Why is eternal inflation interesting? Eternal inflation fractures space into a multiverse of different regions, each of which exits the eternally inflating bulk at a different time. Making cosmological predictions then becomes complicated: different regions have undergone different inflationary histories which may show up as different structures and inhomogeneities in the late universe. This is sketched in the figure below: the “usual” primordial black hole space time is marked as U1, but where the inhomogeneities are large - i.e. inside the black holes - there are regions which continue inflation eternally (E) or exit in a couple of different fashions (U2, U3). The “new universes” U1 and U2 still see the edge of the E region, which makes them violently inhomogeneous at large scales, incompatible with the cosmos we see around us.
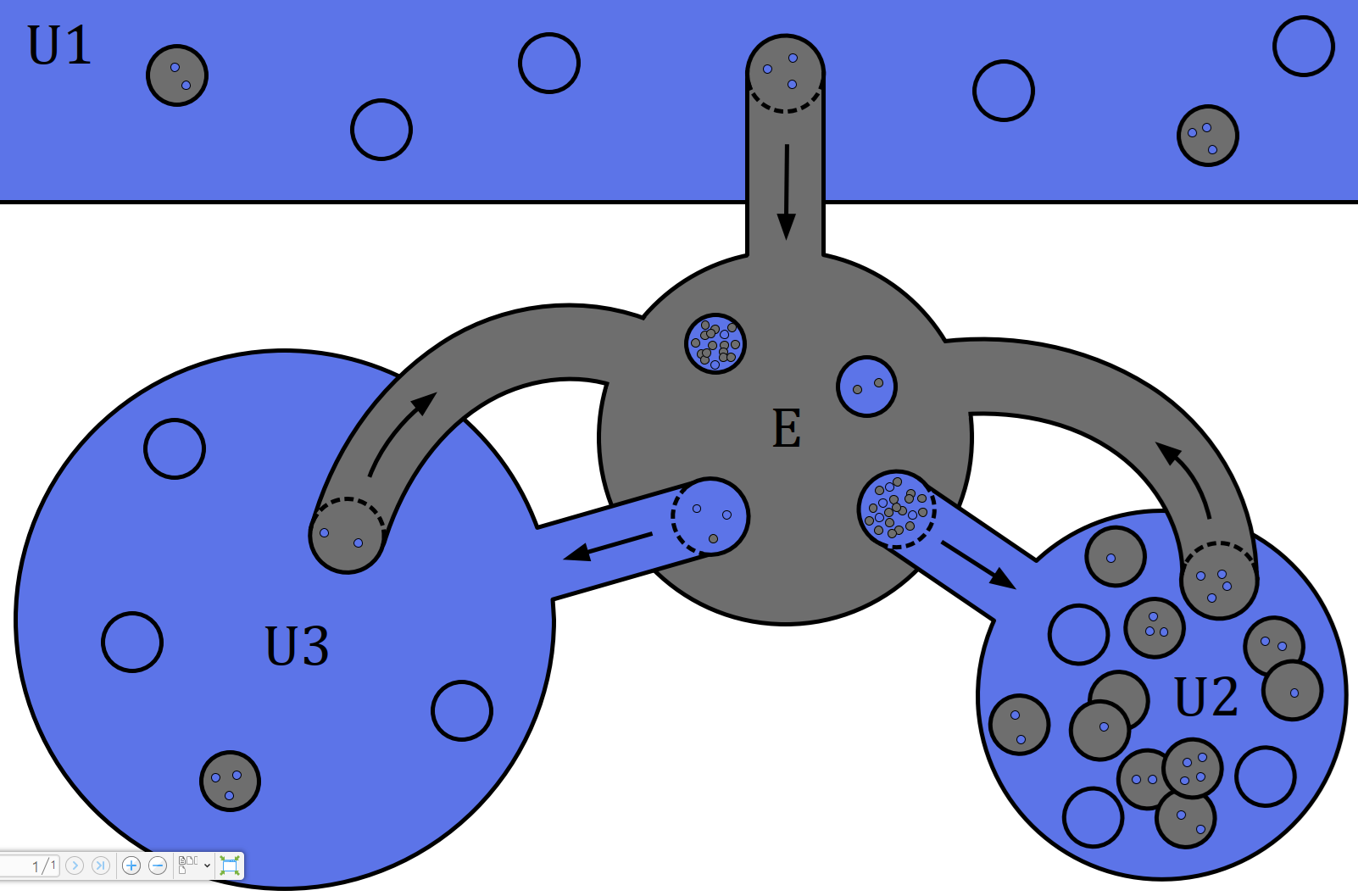
Since the volume of the eternally inflating universe is infinite, it is not easy to assign probabilities for the different universes U1, U2, and U3. This is called the measure problem. However, in our case, all reasonable solutions to the measure problem seem to suggest that the U1 universe (the one that could match our observable universe) is the rarest one, since the others “branch out” of it in an infinite fashion. In other words, eternal inflation presents a challenge to primordial black hole models: the homogeneous pockets of space with black holes are actually the last places we would expect to find ourselves in. To solve this challenge, we may need to consider new types of primordial black hole models or rethink our approach to the measure problem.