We have recently made public a rather technical paper in which we explicitly and unambiguously calculate the cosmic string loop number density distribution in our universe coming from various motivated loop production functions. Such a density distribution crucially determines the spectrum of their emitted gravitational waves, a smooking gun for their potential discovery.
Together with Pierre Auclair, Mairi Sakellariadou and Danièle Steer, we have carefuly explored in Ref.[1] the consequences of changing the slope of the Polchinski-Rocha loop production function to the actual observable cosmic string loop distribution. This is the parameter \(\chi\) in the next plot:
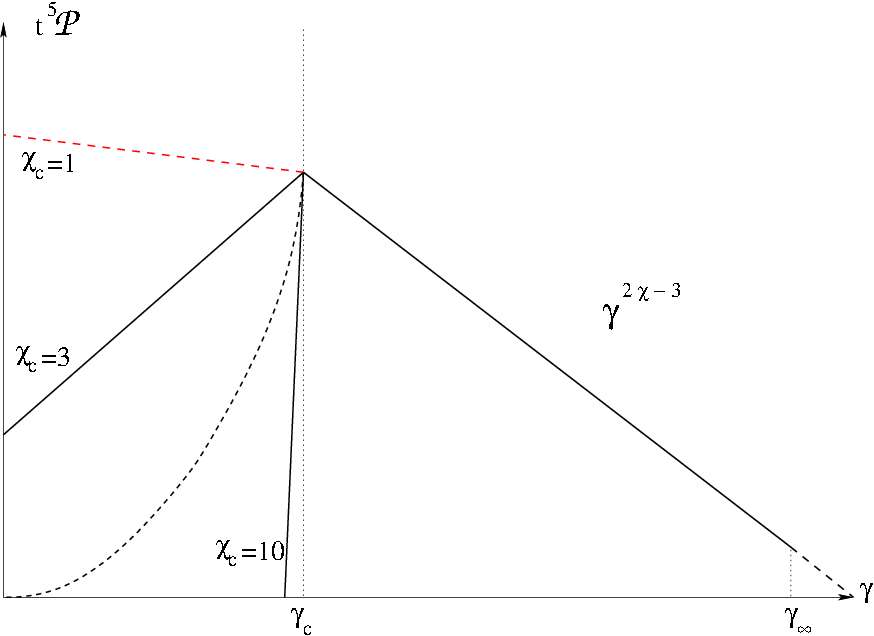
For the cases we have referred to as “sub-critical”, \(\chi < (3 \nu - 1)/2\), corresponding to steep slopes in the previous figure, we recover the results of Ref. [2]. The parameter \(\nu\) encodes the growing rate of the scale factor \(a(t)\), namely, we assume \(a(t) \propto t^\nu\).
For shallower slopes, the so-called “critical” and “super-critical” cases, \(\chi \ge (3\nu-1)/2\), we find that either the loop distribution incessantly grows, or, with some regularisation, reaches a stationnary distribution whose shape depends on what happens on the larger length scales. This is best illustrated by the following plot:
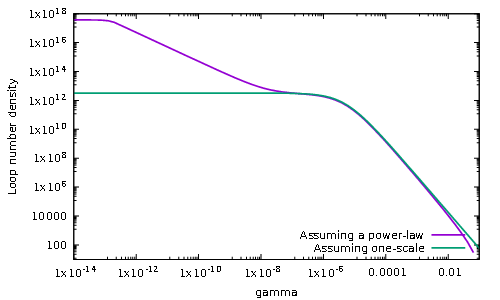
It compares the loop number density produced by assuming an infinitely sharp loop production function peaked at \(\gamma = 0.1\) (green curve) with a (regularised) super-critical Polchinski-Rocha distribution having \(\chi > 0.25\) (purple curve), in the radiation era (\(\nu=1/2\)). As this plot shows, the gravitational backreaction scale, \(\gamma_\mathrm{c}\), at which the loop production function is cut always matters and is responsible for the plateau on the purple curve at small \(\gamma\) values. The existence of a second plateau around \(\gamma \simeq 10^{-6}\) comes from the Infra-Red sensitivity of all super-critical loop production functions.