Stochastic Inflation is a regime of Cosmic Inflation in which quantum fluctuations dominate over the semi-classical evolution. If triggered, it can create strong inhomogeneities and, possibly, a multiverse structure with eternally inflating regions. By reversing time, Baptiste and Christophe have developed a new formalism to compute the statistics of these inhomogeneities and apply it to the flat semi-infinite potential where stochastic inflation is purely quantum.
Cosmic Inflation is the currently favoured scenario of the early universe and refers to an accelerated expansion of the spacetime in its earliest instants. See this post for state-of-the-art observational constraints.
Among the simplest inflationary scenarios, the so-called plateau models may exhibit a very flat potential, as it is the case for the Starobinsky model plotted below. Cosmic inflation occurs in the semi-classical regime and cosmological perturbations are generated for field values around \(\phi_*\) (see figure).
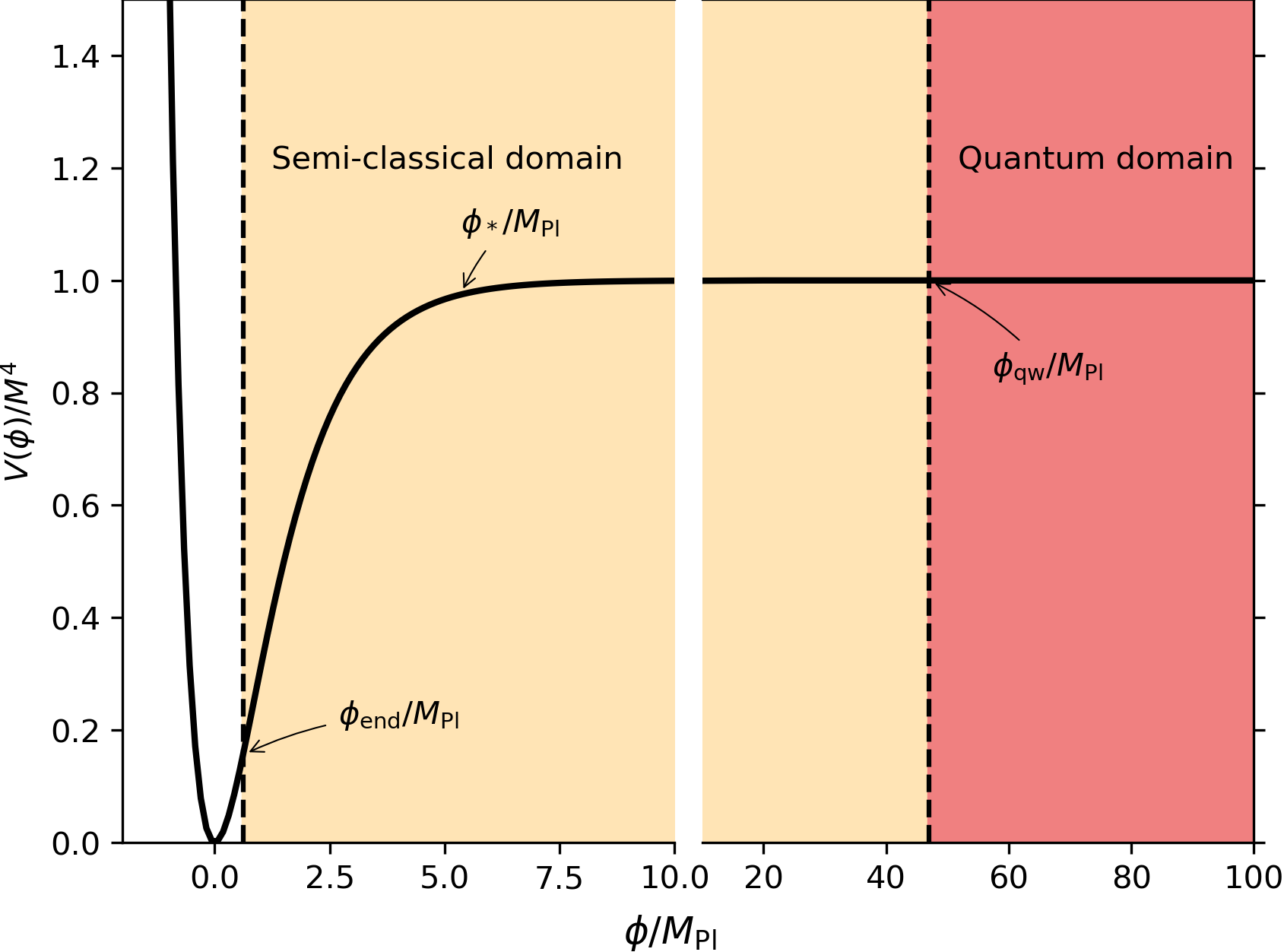
However, there is also a field value, \(\phi_{\mathrm{qw}}\), above which quantum fluctuations dominate, here referred to as the “quantum domain”. The field evolution in there is stochastic, \(\phi\) can move up or down the potential while the universe keeps inflating. The quantum fluctuations being driving the dynamics also implies that the spacetime can become strongly curved, in ways which cannot be easily calculated with semi-classical methods.
Putting numbers together, one finds \(\phi_* \simeq 5 \, M_{\mathrm{Pl}}\) and \(\phi_{\mathrm{qw}} \simeq 47 \,M_{\mathrm{Pl}}\). In other words, the quantum domain is very far away from everything than can be observed in Cosmology. In fact, we can associate some length scales to this region by counting how much semi-classical expansion occurs between \(\phi_\mathrm{qw}\) and \(\phi_*\). We find that the quantum domain may affect our universe on length scales larger than \(10^{10^{16}}\,\mathrm{Gpc}\), a tetration. Therefore, cosmic inflation extended with stochastic inflation implies that quantum physics is in charge not only within the microscopic world but also on the largest possible distances. Why bothering? First, as we discuss in this post, some residual gradients of these inhomogeneities might create a non-vanishing curvature in our observable Hubble volume, and this could be a mean to determine, given some curvature measurement, how likely stochastic inflation is. Then, on more fundamental grounds, this quantum domain is a natural extension of what we expect from cosmic inflation in plateau potentials, understanding the structure of the universe it is creating is what Cosmology is all about.
Working out the dynamics of the field-metric system when \(\phi > \phi_\mathrm{qw}\) can be made using the so-called stochastic inflation formalism (see this post for an application to primordial black holes). It is an effective field theory in which quantum fluctuations on sub-Hubble scales are integrated out to determine the field and metric evolution on super-Hubble scales, the latter emerging as real stochastic variables.
Unfortunately, when applied to a potential \(V(\phi) = 3 H_{\mathrm{inf}}^2\) being exactly constant for \(\phi > \phi_\mathrm{qw}\), stochastic inflation leads to divergences and that is preventing the determination of the spacetime curvature. Indeed, assuming that stochastic inflation started at \(\phi_0\), at a time \(N_0\), it stops when the quantum fluctuations push the field away from the quantum domain, i.e. when \(\phi = \phi_{\mathrm{qw}}\) at a time \(N_{\mathrm{qw}}\). Using the stochastic formalism, one can show that the mean value of the lifetime
\[\langle N_{\mathrm{qw}}-N_0\rangle = \infty.\]In other words, stochastic inflation lasts, on average, an infinite amount of time. However, we are necessarily living in one of the realizations in which stochastic inflation ended. As such, when concerned with cosmological observables, we should only be concerned with the set of all quantum realizations in which stochastic inflation ends.
A way to enforce the ending condition is to reverse the flow of time: the quantum field starts at \((\phi_{\mathrm{qw}},N_{\mathrm{qw}})\) and evolves backward in times to end its evolution at \((\phi_0,N_0)\). Even if the idea is very simple, its practical implementation requires to mathematically perform what is called a time-reversion in diffusion processes. This is what we have done in Ref. [1] for stochastic inflation by reversing from the lifetime. Defining the reverse time by
\[\Delta N \equiv N_{\mathrm{qw}} - N,\]together with \(\Delta \phi \equiv \phi - \phi_{\mathrm{qw}}\), the field value in reference to the quantum wall, the following picture shows one of these reverse-time realization.
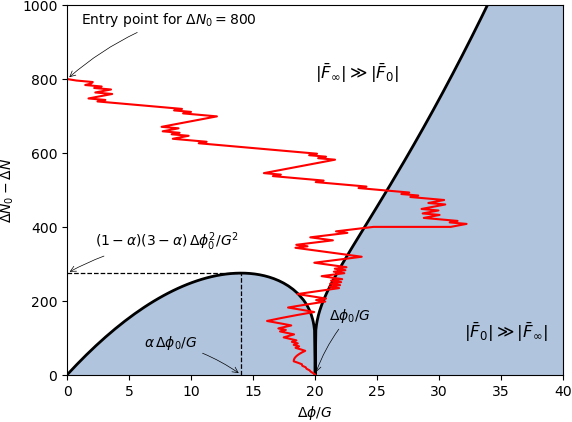
This trick allows us to interpret stochastic inflation as a collection of random processes conditioned by their lifetimes \(\Delta N_0\). On the mathematical side, the associated probability distribution \(\bar{P}(\phi,\Delta N|\phi_0,\Delta N_0)\) has been shown to follow a reverse Fokker-Planck equation that we have solved, one of the solution being represented below. The colors encode how probable it is to find the field at a given value, at a given reverse time, and for a given lifetime \(\Delta N_0\) of the processes.

In the reverse-time stochastic inflation formalism, all divergences are gone and we were able to determine the distribution \(P(\zeta|\phi_0)\) of the spacetime curvature fluctuations \(\zeta\). It is a well-defined and normalizable distribution, which has been obtained by marginalization over all possible lifetimes, including the infinite limit. We find that it depends on one parameter only, the initial field excursion value \(\Delta \phi_0 = \phi_0-\phi_{\mathrm{qw}}\) expressed in unit of the Hubble parameter during inflation, i.e. the quantity
\[\chi_0 \equiv \frac{2\pi \Delta \phi_0}{H_{\mathrm{inf}}}.\]The probability distribution for \(\zeta\) is plotted below as a blue curve.
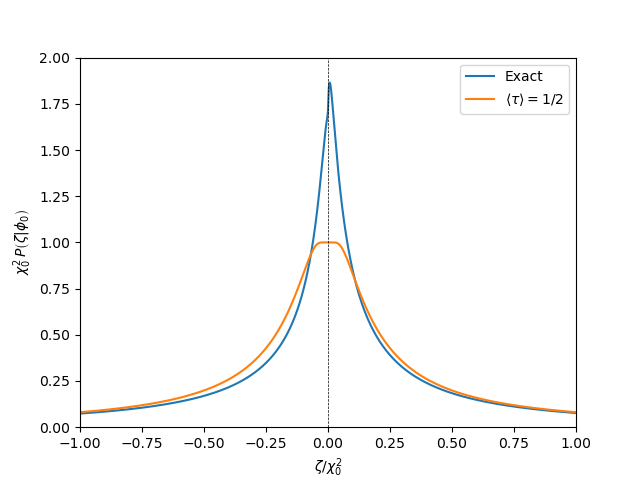
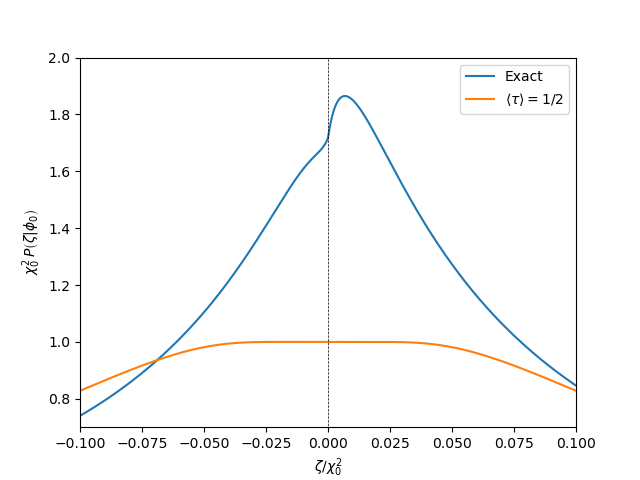
It is skewed towards positive values and has tails slowly decaying as \(|\zeta|^{-3/2}\). The orange curve is an analytical approximation matching very well the exact distribution in the tails. It reads
\[\chi_0^2 P(\zeta|\phi_0) \simeq \mathrm{erf}\left(\frac{\chi_0}{2\sqrt{|\zeta|}}\right) - \frac{\chi_0}{\sqrt{|\zeta|}} \dfrac{\exp{\left(-\frac{\chi_0^2}{4|\zeta|}\right)}}{\sqrt{\pi}}.\]In qualitative terms, our result shows that nothing really bad occurs when stochastic inflation occurs within the flat semi-infinite potential. The distribution of \(\zeta\) ends up being peaked around vanishing values with a width typically given by \(\chi_0^2\). As such, it is very well possible that our observable universe is a classical slice sandwiched between two quantum worlds, the very small and the very large!