In a recent preprint, Cristian and Sébastien show the robustness of Starobinsky and Higgs inflation to inhomogeneous initial conditions of all sizes. They have performed full numerical relativity simulations with strong inhomogeneous initial field and velocities. After some “wibbly-wobbly timey-wimey” evolution, the system relaxes towards… Cosmic Inflation.
Their results are presented in Ref. [1]. Simulations show that sub-Hubble, as well as Hubble-sized, fluctuations generically lead to inflation after an oscillatory phase between gradient and kinetic energies. The following figure shows the evolution of the equation of state for sub-Hubble (top), and super-Hubble (bottom) inhomogeneous initial conditions.
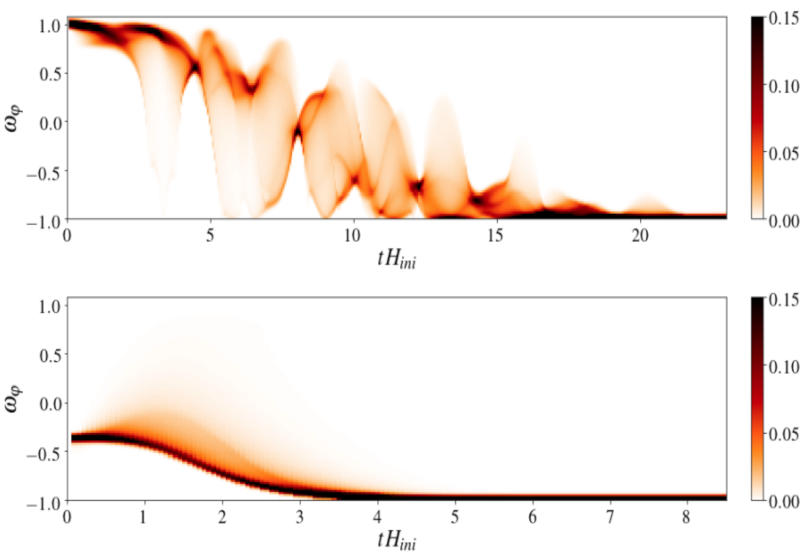
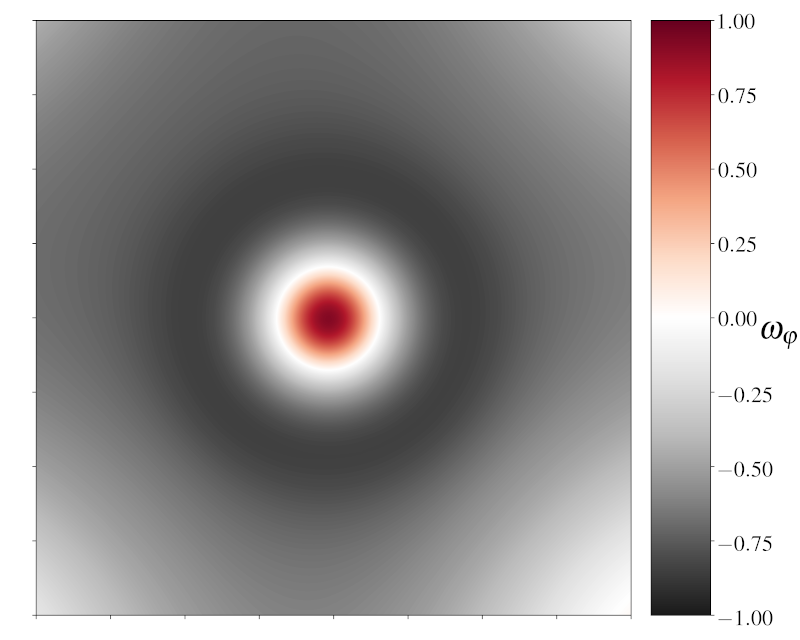
Whilst Hubble-sized fluctuations are able to form large pre-inflationary black holes, their horizons end up being always sub-Hubble and this allows for inflation to take place in the neighbourhood of the black hole horizon. These results could even suggest that the formation of large pre-inflationary black holes can catalize the onset of inflation. They trap gradient energies and therefore smooth the field and metric in the surrounding regions. An equatorial slice of a black hole forming is represented below.
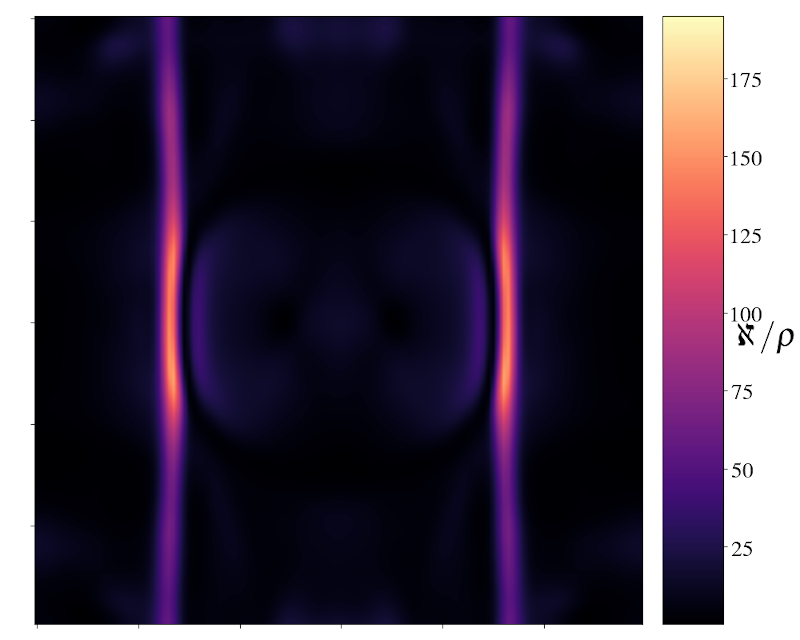
Paradoxically, when inhomogeneities escape the formation of black holes, the dynamics becomes the richest. On sub-Hubble scales, the non-linear dynamics of the deeply inhomogeneous scalar field sources metric backreactions in the form of shear and tensor modes. These modes are found to decay slower than the energy density of the field and can potentially dominate the energy content of the Universe for a while. However, when this occurs, the beginning of inflation is simply delayed but never prevented. The next figure represents a snapshot of the gravitational modes “energy” produced in the sub-Hubble dynamics.
Our analysis further supports the robustness of inflation to any size of inhomogeneity, in the field, velocity or equation-of-state. At large scalar field values, the pre-inflation dynamics only marginally depends on the field potential and it is expected that such behaviour is universal and it applies to any inflation potential of plateau-type, as the ones favoured by the CMB observations after Planck.