Cosmic Inflation, the most favoured scenario of the early Universe, implies that all forms of matter and radiation observed today are the outcome of quantum fluctuations occurring around the event horizon of a exponentially fast accelerating space-time. Clearing the ground for the incoming spatial and ground based cosmological observations, Pierre and Christophe have derived, at an unprecedented level of precision, the shape of the expected power spectra of both the quantum-generated gravitational waves and curvature perturbations.
Cosmic Inflation is an hypothetical early phase of accelerated expansion that has occurred before the first billionth of a second of existence of our Universe. It provides a natural mechanism to explain the observed flatness of our Universe today and naturally solves the so-called horizon problems of the Big-Bang model.
In a spectacular way, the quantum fluctuations that are inherently sourced during the inflationary era are exactly what is needed to explain the origin of the cosmological perturbations: the seeds of the galaxies of today.

These quantum fluctuations are deeply rooted in gravity and appear as both primordial gravitational waves \(h_{ij}\) and curvature perturbations \(\zeta\), with very peculiar correlation functions. In Ref. [1], we have pushed to third order the calculation of these correlation functions. They are completely determined by the Hubble parameter during inflation \(H(N)\) and its logarithmic derivatives, \(\epsilon_i(N) \equiv \mathrm{d}\ln H / \mathrm{d} \ln N\) (the so-called Hubble flow functions). Here \(N=\ln a\) is the logarithm of the scale factor \(a\).
Slow-roll inflation predicts the correlation functions to be given by these spectra:

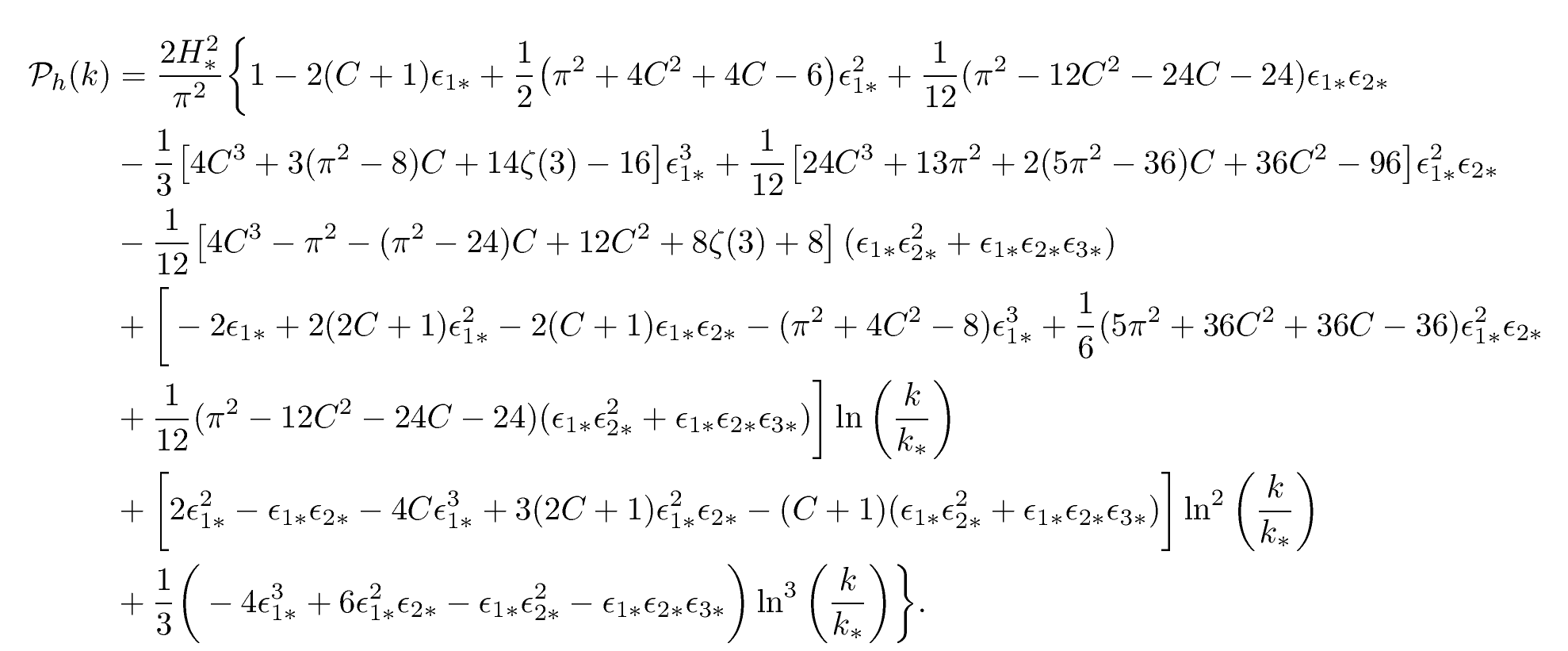
They are expanded around an observable wavenumber \(k_*=0.05\,\mathrm{Mpc}^{-1}\) and readily testable with the incoming cosmological observations from the Euclid and LiteBird space telescopes, but also from the ground based CMB-S4 telescopes and Simons Observatory. Are we going to detect a non-vanishing \(\epsilon_{3*}\)?