Could cosmological perturbations stretched over distances larger than the size of the observable Universe modify the shape of our space-time? Baptiste, Pierre and Christophe, in collaboration with Vincent Vennin, have recently shown that this is the case through the spatial curvature.
It is a common Cosmologist’s intuition that cosmological fluctuations, the tiny perturbations of amplitude \(10^{-5}\) at the origin of galaxies, should induce some kind of noise on the cosmological parameters. Is this quantifiable? Are super-Hubble cosmological perturbations having an effect at all?
In Ref. [1], we show that arbitrarily long perturbations have an observable effect. More precisely, the gradient and Laplacian of these fluctuations are dynamically creating a spatial curvature in the homogeneous and isotropic metric of local observers. In the following picture, we sketch how one of these modes, having a wavelength much larger than the observer’s Hubble radius, can be “felt” through its gradient.

It is not a few Hubble-sized fluctuations that contribute, but an infinite number of super-Hubble modes, all those having wavelength larger than our observable universe. Denoting by \(K\) the curvature of the FLRW spatial sections, and \(\xi\) the sum of these constant modes, we find
\[K = -\frac{2}{3} \Delta \xi - \frac{1}{3} \left(\nabla \xi \right)^2.\]However, because fluctuations are, by definition, of random nature, we cannot predict a definite value for the curvature density parameter \(\Omega_\mathrm{K_0}\). This one is now promoted to a stochastic variable. Even though the sum of all super-Hubble modes averages to zero, i.e. \(\langle \xi \rangle = 0\), we predict, for the standard Gaussian and scale-invariant cosmological perturbations, a very small non-vanishing value
\[\langle \Omega_\mathrm{K_0} \rangle = -\frac{\langle K e^{-2\xi} \rangle}{a_0^2 H_0^2} = \frac{5}{6} \mathcal{P}_* \simeq 1.7 \times 10^{-9}.\]More importantly, because \(\Omega_\mathrm{K_0}\) is a stochastic variable, it also fluctuates and its realizations are, in fact, dictated by its standard deviation
\[\sqrt{\langle{\Omega_\mathrm{K_0}^2}\rangle-\langle{\Omega_\mathrm{K_0}}\rangle^2} \simeq \dfrac{1}{3} \sqrt{\mathcal{P}_*} \simeq 1.5 \times 10^{-5}.\]This is the typical value that any observer will measure at any epoch during the cosmic history.
But there is more. The spatial curvature of our local Hubble patch is thus a measurable number that can tell us what is going on on the largest possible length scales of the Universe, length scales that are much larger than our Hubble volume. What if the infinite sum of very large wavelength modes, \(\xi\) here, is no longer a small quantity? Such a situation could very well be happening if the Universe has experienced a period of stochastic inflation in its infancy!
In Ref. [1], we have been able to estimate the full probability distribution function for \(\Omega_\mathrm{K_0}\) when cosmological fluctuations are generated by Cosmic Inflation. If \(\xi\) remains small, it is a slightly distorted Gaussian distribution with a typical width of \(10^{-5}\), as expected. But if inflation last for a long period, enough for \(\xi\) to be of order unity, the distribution becomes highly non-Gaussian, as represented in the following figure (red curve)
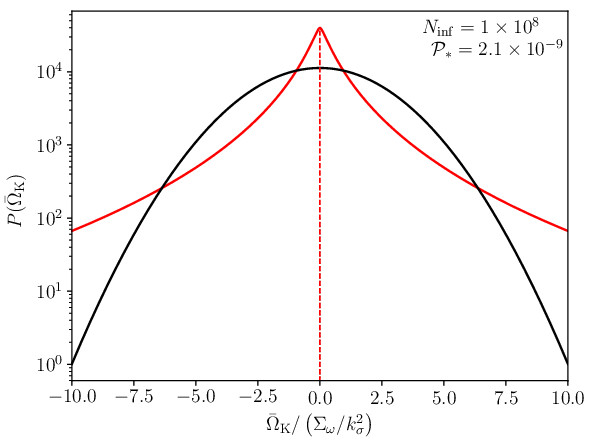
In this plot, the black curve is what would be a Gaussian probability distribution with same width. Clearly, large values of \(\Omega_\mathrm{K_0}\) are now much more probable than what one could have naively expected. Are we going to measure a non-vanishing \(\Omega_\mathrm{K_0}\) in the future?