Within the landscape of single-field slow-roll models, and given the present cosmological data, we show that Cosmic Inflation predicts a small negative running of the spectral index of the cosmological fluctuations. This quantity imprints the large scale structures of the universe and we have just made a prediction for its value. Will it be measured negative and small?
In inflationary cosmology, cosmic structures like galaxies find their origin in the quantum fluctuations occurring in the first instants of the universe history. Large and small structures today, represented in the following figure by two length scales \(\lambda_1\) and \(\lambda_2\), do not exit the Hubble radius during inflation at the same times. This time-shift at Hubble exit, combined with a small change of the Hubble radius itself, explains why cosmic structures are aggregated slightly differently at large and small distances. In technical terms, the power spectrum of the cosmological fluctuations is not scale invariant but has a spectral index which is, according to current observations, slightly red \(n_\mathrm{S} \lesssim 1\).
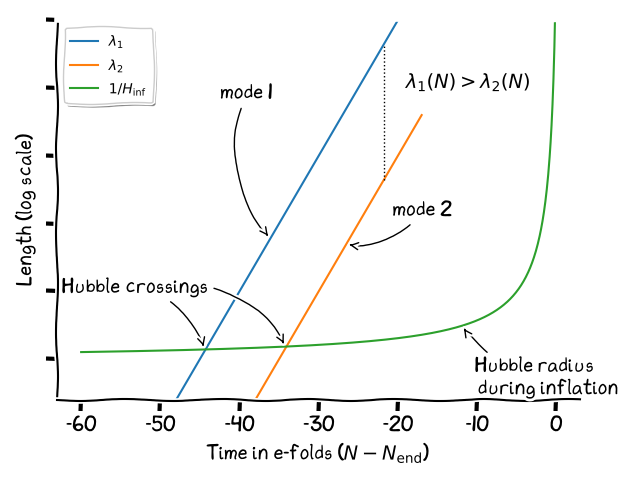
The condition \(n_\mathrm{S} \lesssim 1\) is a “natural” expectation of the single-field scenarios depicted in the previous picture. Indeed, the accelerated slow rolling of the field along its potential necessarily triggers a small growth of the Hubble radius during inflation. Other inflation models do exist in which the slow rolling is actually decelerated and their predicted spectral index ends up being blue (\(n_\mathrm{S} \gtrsim 1\)). These models are however strongly disfavoured since the first measurements of \(n_\mathrm{S}\) by the WMAP satellite (see also this post).
As can be seen in the previous figure, not only the Hubble radius grows but it also accelerates towards the end of inflation. This acceleration implies that the spectral index itself cannot be scale invariant, it should vary with length scales, and that is the definition of the running \(\alpha_\mathrm{S}\). As such, if our understanding of inflation is correct, measuring a red spectral index \(n_\mathrm{S} < 1\) necessarily implies a negative running \(\alpha_\mathrm{S} < 0\).
In Ref. [1], Christophe, Jérôme Martin and Vincent Vennin have computed the marginalized posterior probability of the running of the spectral index \(\alpha_\mathrm{S}\) given the latest Cosmic Microwave Background and Baryon Acoustic Oscillations measurements (see this post for more details on the cosmological data used). The probability distribution is represented below, along with various credible intervals, showing that single-field inflationary models predict a negative running.
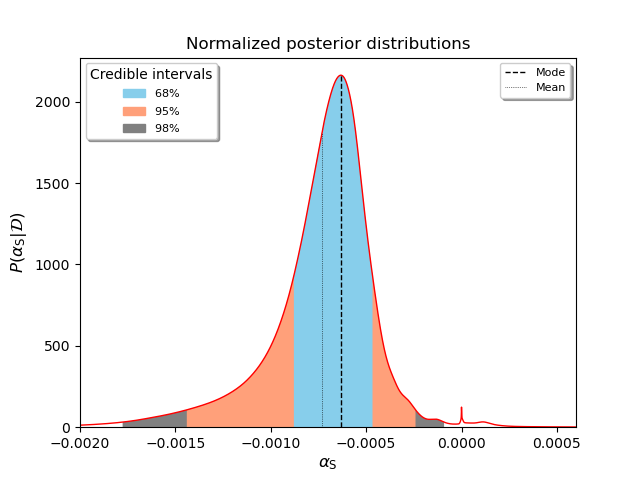
In numbers, we find (confidence given in parenthesis):
\[-8.8 \times 10^{-4} < \alpha_\mathrm{S} < -4.7 \times 10^{-4} \quad (68\%),\] \[-1.4 \times 10^{-3} < \alpha_\mathrm{S} < -2.4 \times 10^{-4} \quad (95\%),\] \[-1.8 \times 10^{-3} < \alpha_\mathrm{S} < -9.1 \times 10^{-5} \quad (98\%).\]These credible intervals are actual predictions and result from the current data being analysed under the theoretical prior that inflation is in the landscape of the slow-roll single-field models. As such, they are highly non-trivial.
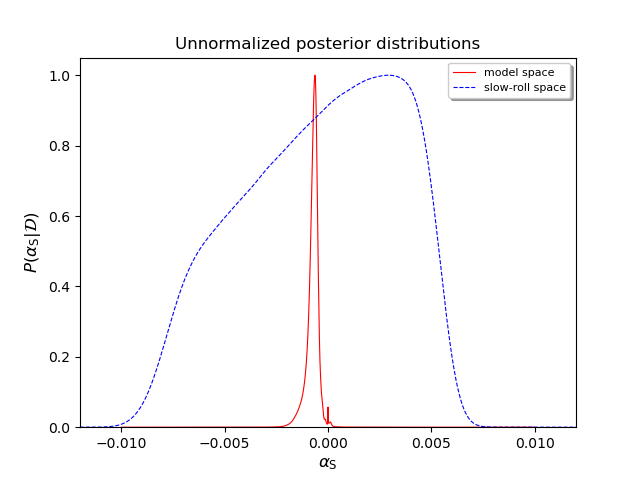
For instance, dropping information from data, or, from the theoretical prior, would let us without any determination of the sign of \(\alpha_\mathrm{S}\). The following figure shows the posterior obtained by not assuming any specific inflationary scenario (“just slow-roll”) as a dashed blue curve. The posterior plotted earlier is reported here as a solid red curve (labelled “model space”). Allowed values of \(\alpha_\mathrm{S}\) under the “just slow-roll” hypothesis are orders of magnitude larger and the sign can be positive or negative.
If, instead, we drop the data while keeping the theoretical prior to be single-field models, one gets

The credible intervals are reported and they show that positive values of the running are allowed within the prior. Therefore, only the combination of the current cosmological data and the hypothesis that inflation occurred within the landscape of single-field models allows us to make the prediction that the running is negative.