A cosmic strings network present in our Universe should be incessantly emitting gravitational waves. An absolute lower limit of the expected signal can be found by determining the gravitational waves created by the back bones of the network: the long cosmic strings. Disrael and Christophe, in collaboration with François R. Bouchet, have computed this irreducible contribution using new numerical simulations of Nambu-Goto cosmic strings.
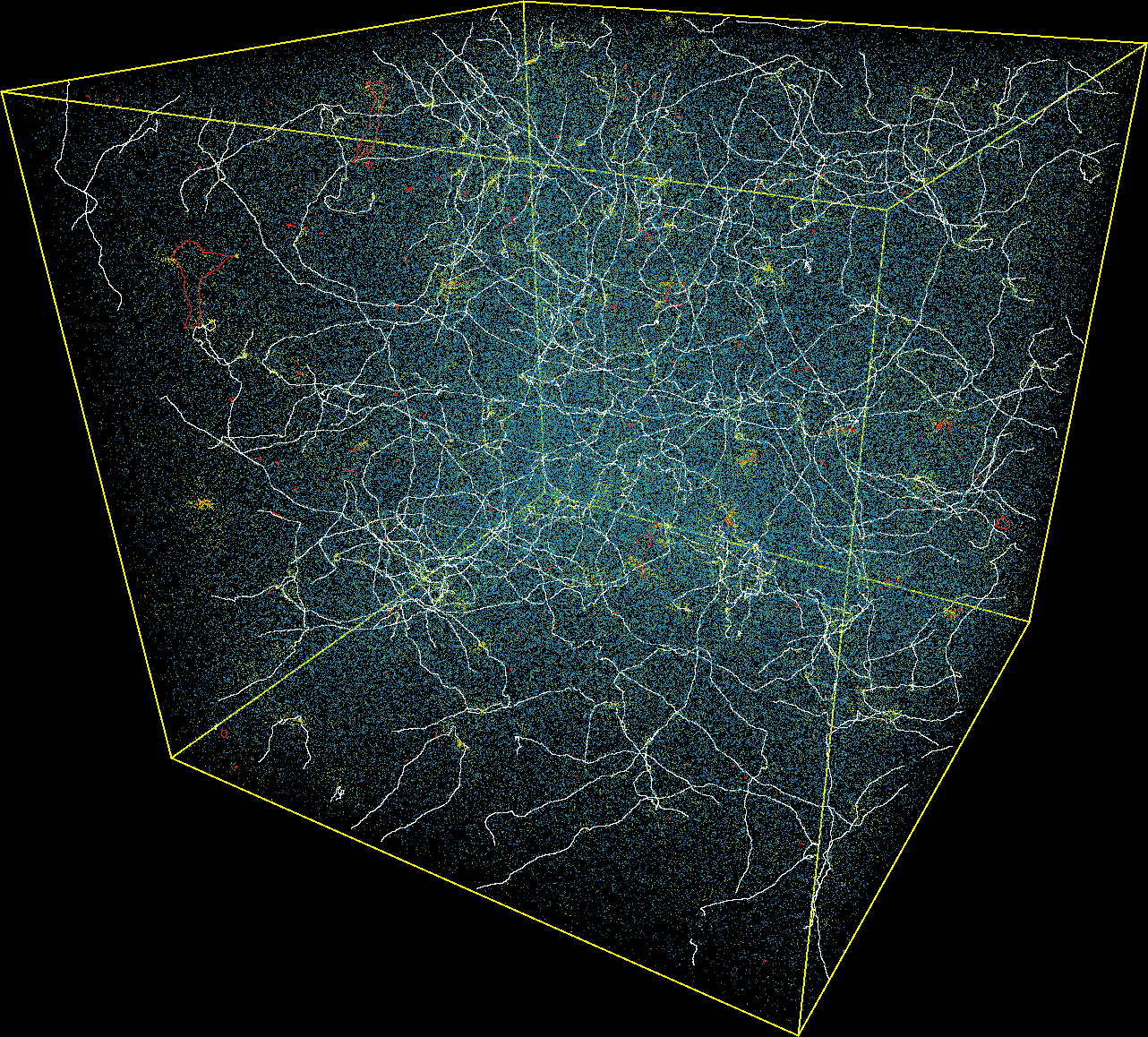
In Ref. [1], we have run new simulations of Nambu-Goto cosmic strings evolving during the radiation, the transition, and the matter eras to compute the unequal time correlators of the anisotropic stress tensor associated with the long strings. The following figure shows a snapshot of one of these simulation, the long strings have been represented in white whereas all the other objects are loops, see Ref. [2] and this post.
This correlator sources the gravitational waves and it allows us to solve for their creation, and propagation, all along the Universe history. By using the Green’s function method we can then predict the strain, \(k^2 \mathcal{P}_h\), and the energy density parameter \(\Omega_{\mathrm{GW}}^{\mathrm{mat}}\) of the gravitational waves that can be measured today. Their power spectra are represented below as a function of the wavenumber \(k\).
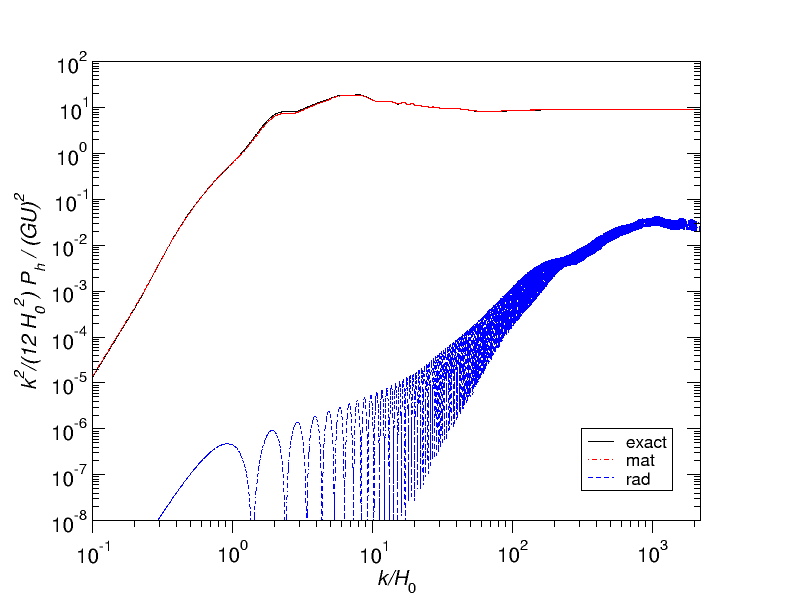
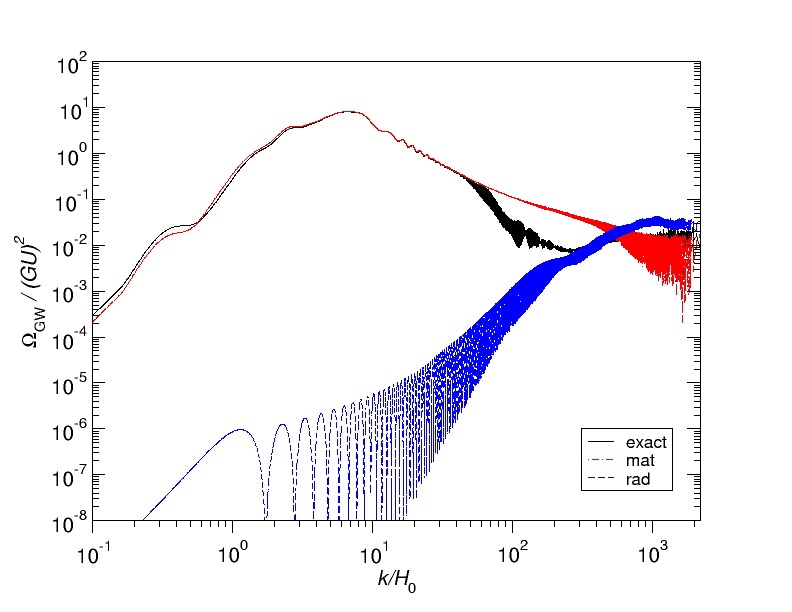
In these figures, the exact numerical result is represented in black while the blue and red curves show some semi-analytical approximations that we had proposed in a previous paper, calibrated using the amplitude found with the simulations, see Ref. [3]. The only significant deviations show up around \(k/\mathcal{H}_0 \simeq 100\), which corresponds to the transition between the radiation and matter era. An interesting point to notice is that most of strain signal is actually generated by the long cosmic strings in the matter era, i.e., close to us.
As we discuss in Ref. [1], this signal is quite small, but reachable by the LISA satellites. These ones will be sensitive to long strings that are undetectable today in the Cosmic Microwave Background.