Are primordial black holes already clustered in the early universe? In a recent publication, Baptiste and Pierre tackle the clustering problem of these enigmatic objects using an excursion-set approach to deal with the so-called “cloud-in-cloud” mechanism.
Primordial black holes (PBH) are cosmological objects that could have been formed in the earliest instants of the universe’s history, for instance, when large overdensities collapse under their own gravity. Understanding how these PBHs cluster is essential as it can provide insights into the evolution of structure formation in the universe and could potentially help in assessing how much, and when, binaries of these objects appear.
In Ref. [1], Pierre and Baptiste have used the excursion-set formalism to quantify the initial spatial clustering of PBHs generated from large Gaussian density fluctuations. Their method takes into account the “cloud-in-cloud” mechanism, which is a critical aspect that is overlooked in studies using the Poisson model of clustering.
In the excursion-set formalism, the collapse of an overdensity to form a PBH of mass \(M\) is recast into the probability of finding the first crossing of a random walk at some scale \(S(M)\). This approach has been already applied to study the formation of large-scale structure, in which multiple crossings of a random walk describe a hierarchy of structures. This formalism was first developed to solve the “cloud-in-cloud” problem, that is resolving this hierarchy of structures.
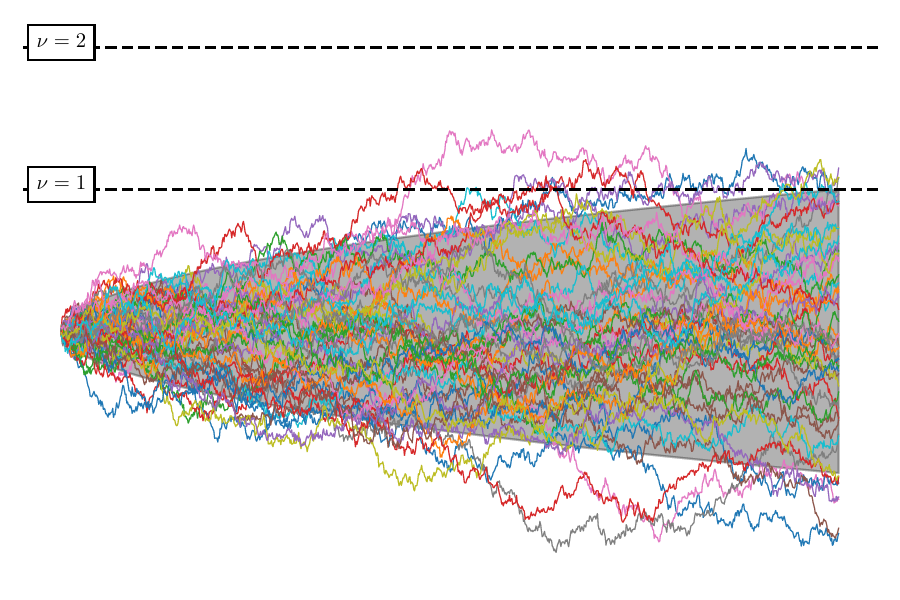
The cloud-in-cloud mechanism implies that PBHs should be part of larger structures: they don’t just appear randomly as per the Poisson assumption. This results in a natural and intrinsic correlation between the formation of pairs of PBHs, which is important for accurately modelling the clustering behaviour at small scales. The following picture shows two random walks that share a common past until the “time” \(S_{r}\): they come from the same realisation of a large scale density perturbation. Subsequently, they evolve in distinct ways and this results in two different collapses that occur respectively at the first-crossing times \(S_{1}\) and \(S_{2}\)

Such an approach automatically includes short-range exclusion effects: PBHs are anti-correlated at short distances!
The authors also present explicit expressions for the excess probability to find pairs of PBHs separated by a given distance and for the excess probability to find pairs with an asymmetric mass ratio.