Making observable predictions for cosmic inflation requires determining when the wavenumbers of astrophysical interest today exited the Hubble radius during the inflationary epoch. These instants are commonly evaluated using the slow-roll approximation and measured in e-folds time. Pierre, Baptiste and Christophe propose a new analytical method to determine these instants with a precision reaching the tenth of an e-fold.
Cosmic Inflation is the leading explanation for the origin of cosmic structures: these are seeded by quantum fluctuations occurring around the event horizon of a exponentially fast accelerating space-time, see this post. By measuring the distribution of galaxies in our universe, the Euclid satellite is expected to provide very soon new exquisite measurements of these fluctuations. Testing cosmic inflation will therefore require to have exquisite predictions as well.
Observable predictions currently rely on the slow-roll approximation to determine the so-called e-fold times \(\Delta N=N−N_\mathrm{end}\), in reference to the e-fold \(N_\mathrm{end}\) at which inflation ended. These instants are actually used to map structures in the sky to quantum fluctuations during inflation. The precision at which they are determined is not so good, they are typically known at \(\mathcal{O}(1)\) e-fold precision. The following figure uses a full numerical integration of various inflationary models to compute the error made (vertical axis) using the slow-roll approximation as a function of the exact timing (horizontal axis).
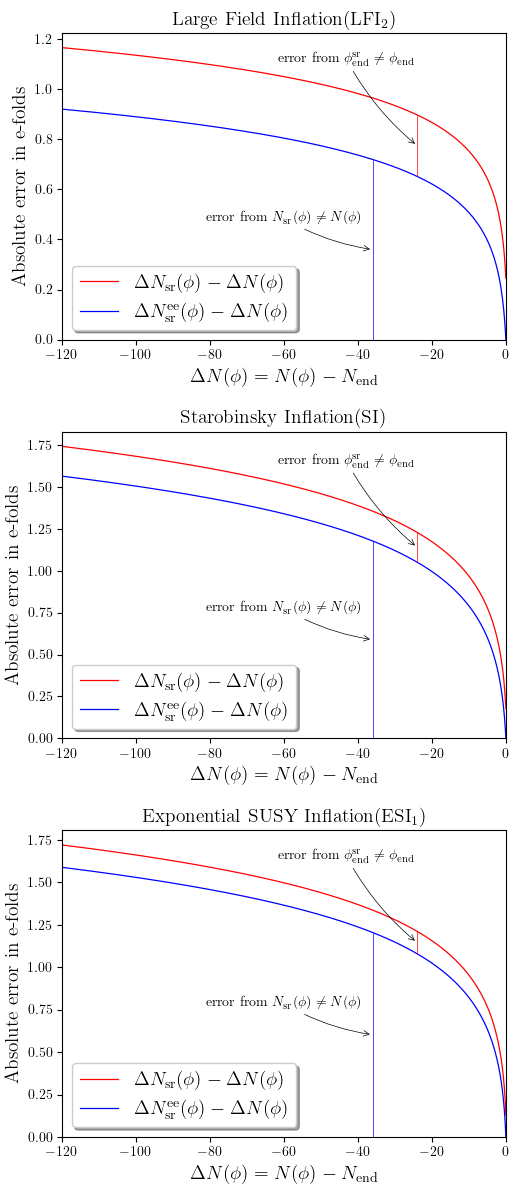
In Ref. [1], we propose a new and simple velocity correction, on top of slow-roll, that increases by one order of magnitude the precision on \(\Delta N\). As shown in the following figure, when compared to the exact solution, our new method reaches an precision of about a tenth of e-fold (blue curve compared to the red one).
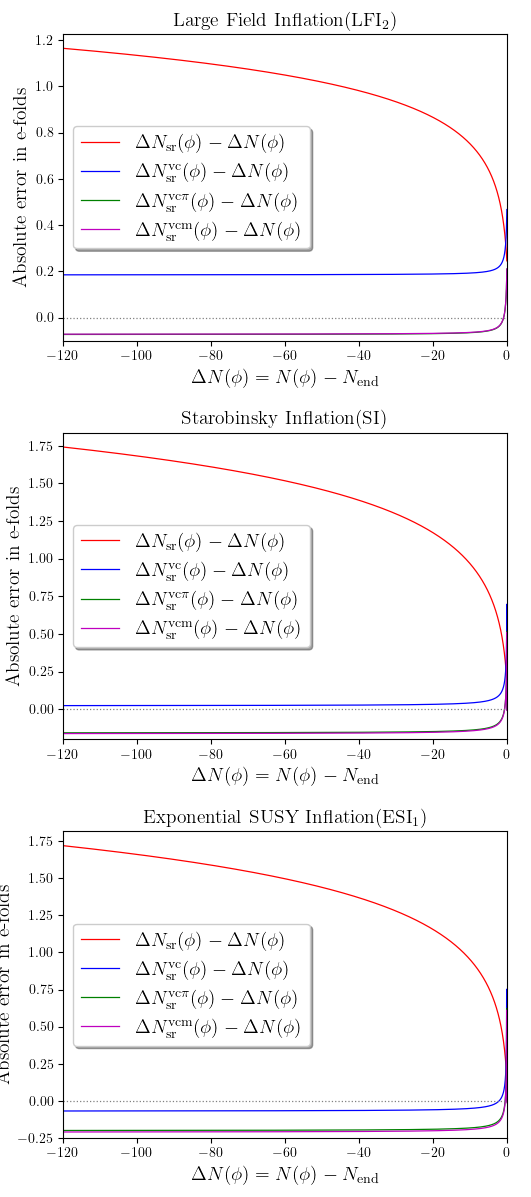
The other curves (green and purple) show other corrections, improving the determination of \(\phi_\mathrm{end}\), the field value at which inflation ends. These ones may, or may not, improve over the velocity correction, depending on the model at hand.