In a recent publication, Chiara, Pierre and Baptiste, together with Vincent Vennin, have developed a novel framework to implement stochastic inflation on random trees. These trees represent dynamically how different regions of space grow and gradually become causally disconnected.
Cosmic Inflation is a hypothetical early phase of accelerated expansion that occurred before the first billionth of a second of existence of our universe. It provides a natural mechanism, quantum fluctuations, to seed the galaxies of today, see this post.
Traditionally, these quantum fluctuations are modeled using a semi-classical perturbative approach, assuming they are small enough not to significantly affect the background metric. However, if perturbations grow large enough, they start influencing the overall structure of spacetime and this is where non-perturbative methods come into play.
Stochastic inflation is a non-perturbative treatment that models cosmic inflation as a stochastic process, much like a random walk. This approach allows for a description of the universe’s dynamics during inflation capturing both quantum diffusion and backreaction effects.
In this context, we have developed a new framework based on Langevin’s equation to generate stochastic trees, an example of which is given below.
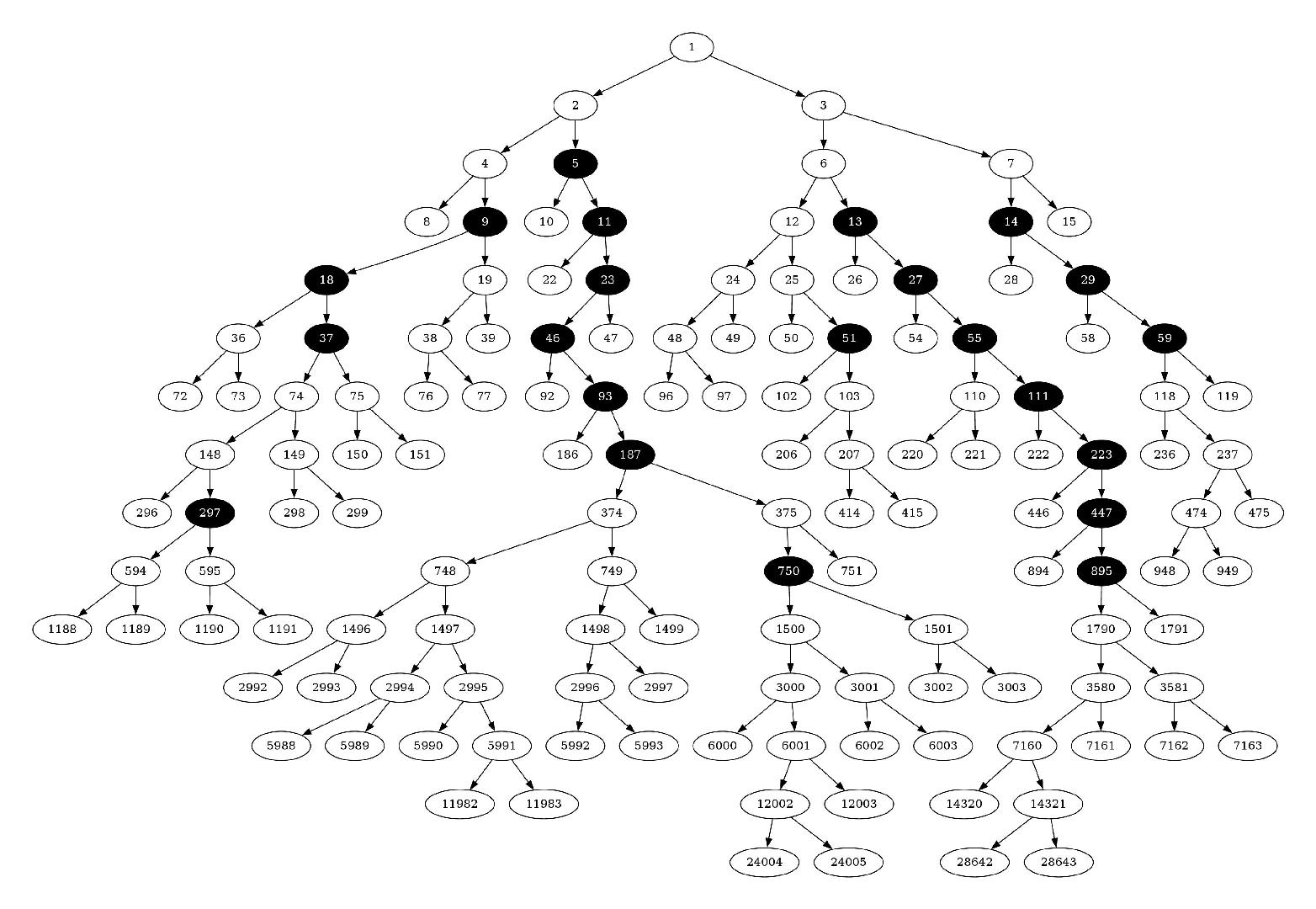
These trees allow for the generation of real-space maps of the curvature perturbation that capture quantum diffusion and its non-perturbative backreaction during inflation. In our approach, we do not need to assume a fixed background, new spacetime units emerge dynamically as the trees unfold, naturally incorporating the metric fluctuations.
To implement this framework computationally, we have developed the FOrtran Recursive Exploration of Stochastic Trees (FOREST) code, which is presented in Ref. [1]. FOREST is designed to efficiently explore and simulate these stochastic trees, providing a powerful platform for studying inflationary dynamics.
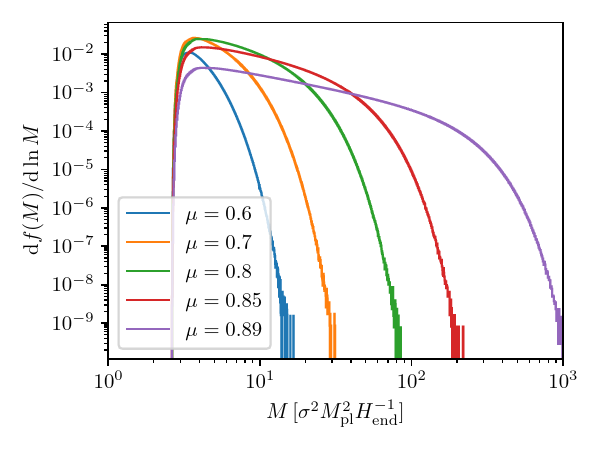
One of the most exciting applications of our method concerns the formation of primordial black holes (PBH) from large curvature fluctuations. In Ref. [1], we discuss why, and how, PBHs can form at the unbalanced nodes in the stochastic trees and FOREST allows us to estimate their mass distribution. The following figure shows a two-dimensional comoving map tracing the curvature perturbations induced by strong quantum effects. These lead to the formation of five PBHs in the darkest regions.
Applied to the “quantum-well” model, a toy setting in which stochastic inflation takes place, we find the PBHs to have masses following a mild power-law distribution terminated by exponential tails. The following figure shows the mass distribution as a function of the size of the quantum well \(\mu\).